1390: IEEE754 부동소수점 표기법
Time Limit: 1 Sec Memory Limit: 128 MBSubmit: 5 Solved: 2
[Submit] [Status] [Web Board] [Creator:]
Description
IEEE 754는 IEEE에서 개발한 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준이다. ±0 등의 수와 무한, NaN 등의 기호를 표시하는 법과 이러한 수에 대한 연산을 정의하고 있다.
IEEE 754의 부동소수점 표현은 크게 세 부분으로 구성되는데, 최상위 비트는 부호를 표시하는 데 사용되며, 지수 부분(exponent)과 가수 부분(fraction/mantissa)이 있다.

기본 형식
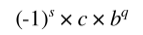
floating point에 대한 표현 방식은 위와 같다.
s : 부호부(sign)를 표현하며 0인 경우 +, 1인 경우 -를 나타낸다.
예를 들자면 1.2345를 밑수가 10인 경우로 표현을 한다면 다음과 같다.
기본 형식에 의해 각 부분의 값은 다음이 된다.
s : 0
실제 표현시에는 IEEE 754에서 정한 정밀도(precision)에 따라 가수부(significand)와 지수부(exponent)의 bit size가 달라지므로 표현하는 숫자의 자릿수가 달라지게 된다.
특수값이 아닌 경우
binary32의 bit 구성은 가수부 23bit, 지수부 8bit, 부호부 1bit로 이루어져있다. 자세한 내용은 도움 참고.
NaN의 조건
c : 가수부(significand, fraction, mantissa)를 나타내며 양의 정수로 표현된다. 정밀도(precision)에 따라 범위가 제한된다.
b : 밑수(ba
q : 지수부(exponent)를 나타내며 지수부는 소수점의 위치를 나타내게 된다.
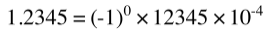
c : 12345
b : 10
q : -4
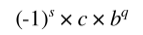
(이때 모자라는 부분은 0으로 채운다.)
Inf의 조건
Input
2진수 문자열 32 비트 정밀도의 0과 1로 이루어진 문자열이 제공된다.
Output
또는 NaN 또는 ±Inf
0의 경우 부호에 상관 없이 0을 출력한다.
Sample Input Copy
4
11000011100111010101000000000000
11111111110000000000000000000001
11111111100000000000000000000000
10000000000000000000000000000000
Sample Output Copy
-314.625
NaN
-Inf
0
HINT
임의의 실수 -12.375를 binary32 형식으로 표현해 본다.
binary32의 bit 구성은 위의 표에 의하면 가수부 23, 지수부 8, 부호부 1가 필요하므로 이를 도식으로 나타내면 다음과 같다.

먼저 임의의 실수에서 부호부를 bit로 표현하면 -12.375는 음수이므로 부호부(sign)의 bit 값은 1이 된다.

절대값 12.375를 이진법으로 표현하면 1100.011이 된다.
참고로 이진법으로 변환할 때 소숫점 앞의 정수부는 나머지가 2보다 작을때까지 나눈 나머지들로 표현을 하고 소숫점 뒤의 소수부는 결과가 1.0이 될때까지 2를 곱하여 각 단계별 정수부로 표현을 한다.
이제 결과를 정규화(normalize) 한다. 정규화란 산술표현시 가수부(c)의 맨 앞자리가 1이 되도록 처리하는 것을 뜻한다. 정규화가 되면 가수부(c)는 1.xxxx 식으로 표현된다.
앞의 결과를 정규화하면 다음과 같다.
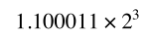
정규화를 하게되면 가수부의 정수부는 항상 1이 되므로 binary32 표현시 생략한다.
binary32 형식은 가수부가 23 bit로 구성되어있지만 정규화 작업에 의해 가장 앞의 1은 생략하여 표현하므로 실제로는 24bit를 표현하고 있는 것이다. 이러한 방식을 숨겨진 bit(hidden bit)를 사용한다고 말한다.
이제 가수부를 표현하면 다음과 같다.

이제 지수부만 남았다. 지수부는 양수/음수 모두 가능하기 때문에 이를 표현하는 특별한 방법을 사용하는데 IEEE 754에서는 bias 표현을 사용하여 양수와 음수를 표현한다.
binary32 형식에서 지수부는 8 bit로 구성되어있고 최소값은 -126이고 최대값은 127을 갖는다.
8 bit로 표현가능한 값은 0 ~ 255이기때문에 이를 반으로 나누어 양수와 음수를 표현하는 것이다.
즉, bias + q = 지수부(exponent)가 된다.
본 예시에서는 q = 3이므로 bias + q = 127 + 3 = 130이 된다.(Exponent가 8비트이기에 bias는 2^7 -1, 32비트 문제인 이 문제에서는 127만 쓰면 된다.)
130을 이진법으로 표현하면 10000010이다. 이제 마지막으로 지수부를 채워 binary32로 표현하면 다음과 같다.

[ 참고 ]
https://nybounce.wordpress.com/2016/06/24/ieee-754-floating-point%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90-%EC%82%B0%EC%88%A0%EC%97%90-%EB%8C%80%ED%95%98%EC%97%AC/
https://ko.wikipedia.org/wiki/IEEE_754
https://readyfortest.tistory.com/47