Problem C: InterGrid
Time Limit: 8 Sec Memory Limit: 128 MBSubmit: 123 Solved: 5
[Submit] [Status] [Web Board] [Creator:]
Description
인류가 살고 있는 우주와는 평행한 또 하나의 우주는 2 차원으로 이루어져 있다.
먼 미래에 인류는 3 차원에 살고있는 스스로와 인류가 만든 물질의 차원을 축소할 수 있는 방법을 찾아내기에 이르렀고, 아울러 평행하는 우주와 우주 사이를 이동할 수 있게 되었다.
2 차원 평행 우주를 여행하는 임무를 맡은 shake 호는 해당 우주의 지도를 받았다.
그 지도에서 모든 위치는 제 1 사분면에 해당하는 영역의 좌표로 표시한다.
즉, 가장 왼쪽 아래의 지점은 (0, 0)으로 표현하며 오른쪽이나 위로 갈수록 각 축의 좌표가 증가하게 된다.
먼 미래에 인류는 3 차원에 살고있는 스스로와 인류가 만든 물질의 차원을 축소할 수 있는 방법을 찾아내기에 이르렀고, 아울러 평행하는 우주와 우주 사이를 이동할 수 있게 되었다.
2 차원 평행 우주를 여행하는 임무를 맡은 shake 호는 해당 우주의 지도를 받았다.
그 지도에서 모든 위치는 제 1 사분면에 해당하는 영역의 좌표로 표시한다.
즉, 가장 왼쪽 아래의 지점은 (0, 0)으로 표현하며 오른쪽이나 위로 갈수록 각 축의 좌표가 증가하게 된다.

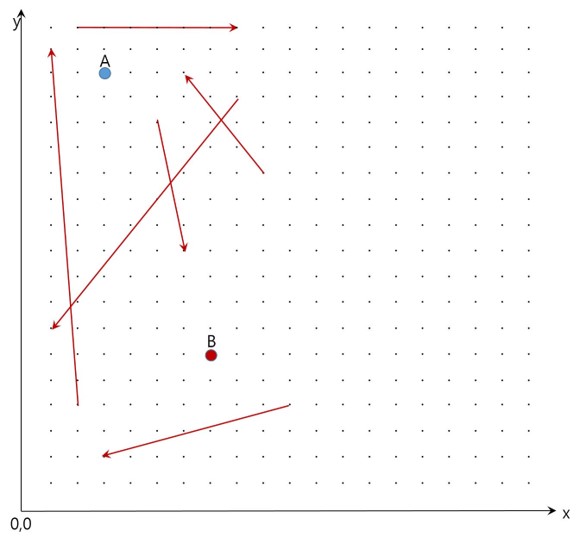
<2차원 우주의 지도 예시>
shake호가2차원 우주에서 각 지점을 이동할 때에는 두 지점 사이의 멘하탄 거리만큼의 에너지를 사용하게 된다.
두 점A(xa, ya)와 B(xb, yb)사이의 멘하탄 거리 D = |xa− xb| + |ya− yb| 이다.
하지만 이 2 차원 우주에는 몇 개의 단방향 웜홀(빨간색 화살표)이 존재하는데, 웜홀을 이용하면 웜 홀의 출발점에서 도착점까지 0 의 에너지를 사용하여 도달할 수 있다.
물론 웜 홀의 출발점에 도달하더라도 무조건 웜 홀을 사용하지는 않아도 된다.
shake 호의 현재 위치 A(xa, ya)와 도달하고자 하는 목적지의 좌표 B(xb, yb)가 주어질 때, 해당위치로 이동할 때 사용해야할 최소의 에너지 사용량을 계산해보자.
Input
첫 줄에는 xa, ya, xb, yb와 2 차원 우주에 존재하는 웜 홀의 개수를 나타내는 정수 N이 주어진다. N은 0 과 5,000 사이의 정수이다.
그 후 N 줄에 걸쳐서 한 줄에 하나씩 웜홀의 출발점 S 와 도착점 F 의 좌표 xs, ys, yf, yf가 주어진다. 2차원 우주의 모든 좌표는 0 과 1,000,000 사이의 정수이다.
Output
첫 줄에 shake 호가 A 지점에서 B 지점으로 이동하기 위해 사용해야 할 최소한의 에너지를 정수 형식으로 출력한다.
Sample Input Copy
3 17 7 6 6
9 13 6 17
5 15 6 10
2 19 8 19
2 4 1 18
10 4 3 2
8 16 1 7
Sample Output Copy
9
HINT
다익스트라 알고리즘